Mathe-SA am 12.06.2025

Funktionen und Graphen

Funktionsgraphen

Name	Funktionsgleichung	Graph
Lineare Funktion	f(x) = k ⋅ x + d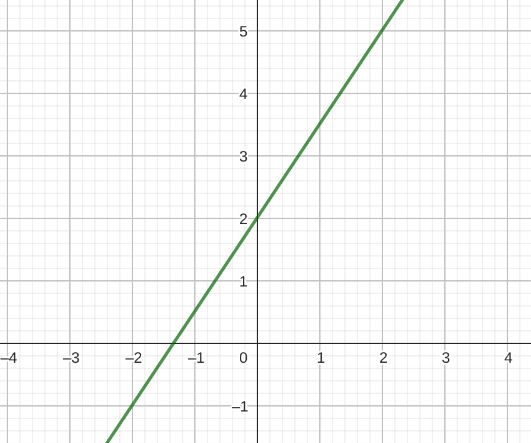
Quadratische Funktion	f(x) = a ⋅ x² + b ⋅ x + c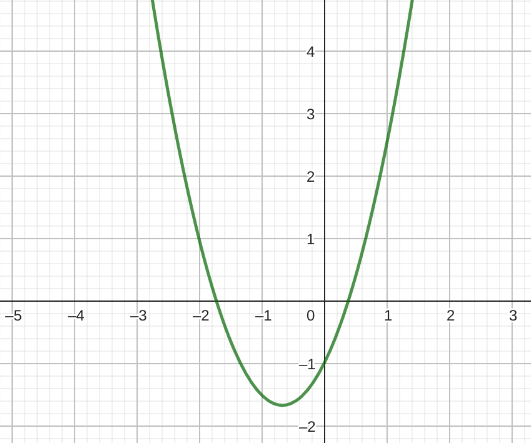
Exponentialfunktion	f(x) = a^x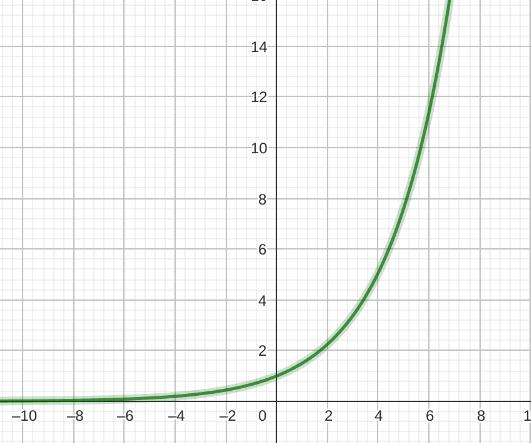
Logarithmusfunktion	f(x) = log_n(x)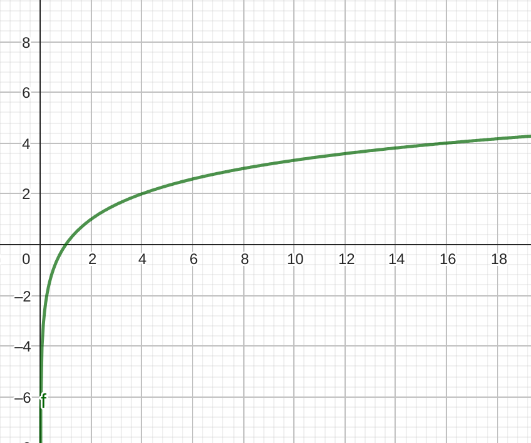
Potenzfunktion Falls n ungerade: "S"-Form Falls n gerade: "W" oder "M"-Form	f(x) = a ⋅ xⁿ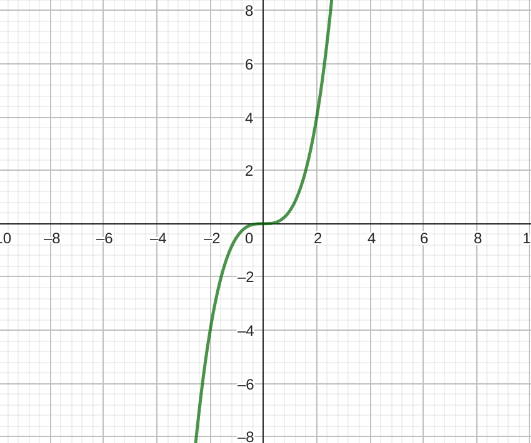
Polynomfunktion Wie bei Potenzfunktion: Falls n gerade: "W" oder "M"-Form Falls n ungerade: "S"-Form	f(x) = a₀ ⋅ xⁿ + a₁ ⋅ x^n-1+ ... + a_n ⋅ x⁰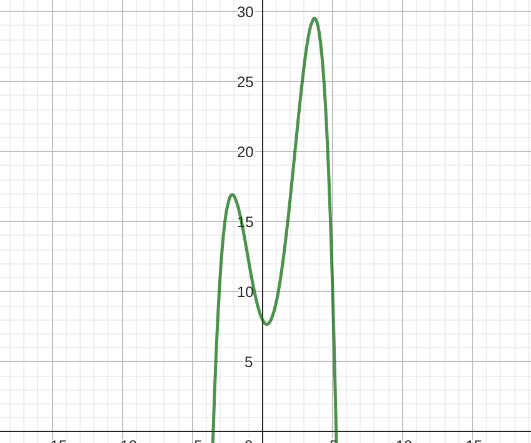

Winkelfunktionen

Sinus- und Cosinusfunktion

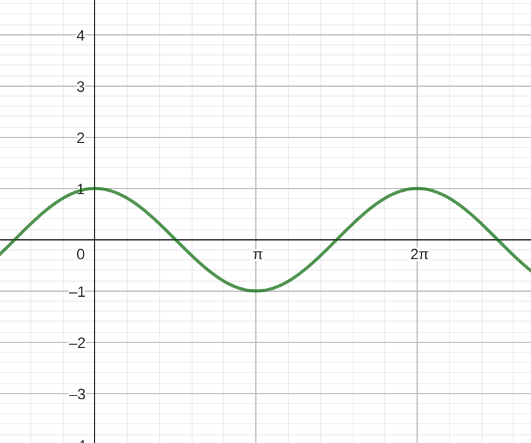
Winkelfunktionen sind Sinus-, Cosinus-, und Tangensfunktion. Diese sehen in der Grundfunktion (Amplitude = 1, keine Phasenverschiebung) folgendermaßen aus:

Sinusfunktion	Cosinusfunktion	Tangensfunktion

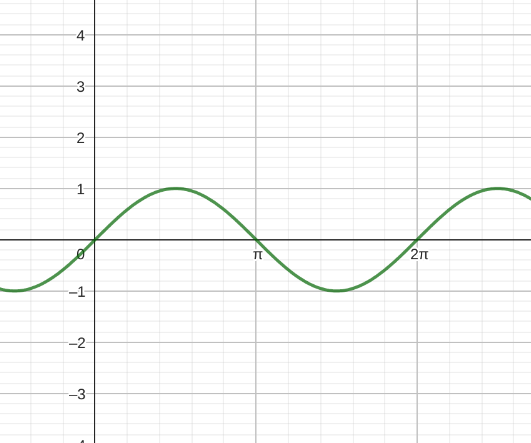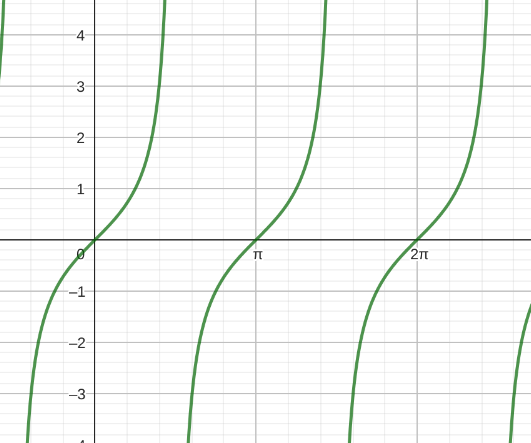Wie man sieht, haben die Sinus- und Cosinusfunktion eine Periode von 2π und die Tangensfunktion eine Periode von π. Die Cosinusfunktion können wir auch als eine Phasenverschobene Sinusfunktion schreiben:

sin(x) = cos(x - $\frac{π}{2}$ ) bzw. cos(x) = sin(x + $\frac{π}{2}$ )

Wie wir sehen, wird die Sinusfunktion bei einer Phasenverschiebung von + $\frac{π}{2}$ um $\frac{π}{2}$ nach links verschoben, die Cosinusfunktion bei negativer Phasenverschiebung nach rechts. Die Sinusfunktion sieht allgemein so aus: f(x) = a ⋅ sin(b ⋅ x + c). a ist die Amplitude, b die Kreisfrequenz, und c die Phasenverschiebung. b kann auch als ω und c als φ geschrieben werden (hauptsächlich in der Physik). Die Amplitude streckt/staucht die Funktion entlang der y-Achse, die Kreisfrequenz entlang der x-Achse. Die Phasenverschiebung verschiebt die Funktion entlang der x-Achse nach links oder rechts.

Schwingungen

Bei harmonischen Schwingungen (also Schwingungen, die durch eine Sinusfunktion s(t) = a ⋅ sin(b ⋅ t + c), also auch Cosinusfunktion, dargestellt werden können) kommen ein paar Begriffe hinzu:

Elongation: Wert der Funktion zum Zeitpunt t
Amplitude (a): Größtmögliche Elongation (höchster Punkt der Funktion)
Schwingungsdauer (T): Zeit, die für eine vollständige Schwingung benötigt wird; ohne Kreisfrequenz ist sie 2π. T = $\frac{1}{f}$ ; T = $\frac{2 ⋅ π}{ω}$
Frequenz: Anzahl an Schwingungen pro Sekunde; Einheit: Hz (Hertz). f = $\frac{1}{T}$ ; f = $\frac{ω}{2 ⋅ π}$

Gleichungssysteme

Für die Schularbeit ist lediglich das Identifizieren eines Gleichungssystems aus einer Textaufgabe und das Lösen dieses Gleichungssystems mithilfe von GeoGebra erforderlich, deshalb wird hier nicht auf das Händische Lösen eingegangen.

Zunächst ist GeoGebra CAS zu öffnen: ☰ oben rechts → Perspektiven → CAS. Dann tippen wir unsere Gleichungen ein und bestätigen jeweils mit "Enter":

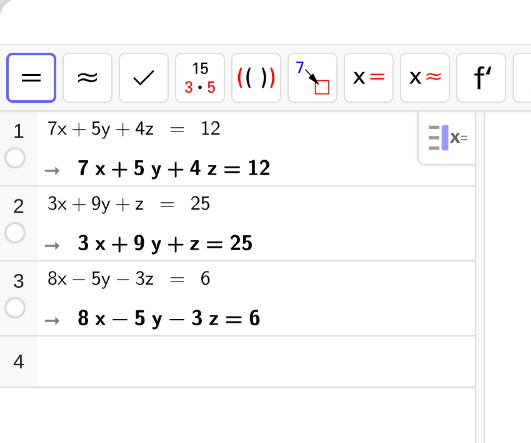
Schlussendlich wählen wir alle Gleichungen aus und klicken auf "x =" im Menü oben links, GeoGebra zeigt uns die Lösung nun automatisch an:

Differentialrechnung

Eigenschaften von Funktionen

Monotonie

Bei normaler Monotonie darf der Funktionswert auch weder steigen noch sinken (gleich bleiben), bei strenger Monotonie muss er durchgehend fallen bzw. sinken:

	steigend	fallend
monoton	Funktionswert wird nicht kleiner	Funktionswert wird nicht größer
streng monoton	Funktionswert wird größer	Funktionswert wird kleiner

Für Montonie wird üblicherweise ein abgeschlossenes Intervall [a; b] angegeben, z.B.: f(x) ist in [a; b] streng monoton fallend.

Extremstellen

Ein Punkt auf einer Funktion in einem Intervall (oder auch allgemein) ist eine Maximumstelle, wenn es im gesamten Intervall keine größeren Funktionwerte gibt. Ein Punkt auf einer Funktion ist eine Minimumstelle, falls es im gesamten Intervall keine kleineren Funktionswerte gibt. Eine Extremstelle ist entweder eine Minimum- oder Maximumstelle der Funktion.

Ein Punkt ist eine lokale Maximumstelle oder Hochpunkt, falls es eine Umgebung des Punktes gibt, in der nur kleinere Funktionswerte vorkommen. Damit ein Punkt eine lokale Minimumstelle oder Tiefpunkt ist, muss es eine Umgebung des Punktes geben, in der nur größere Funktionswerte vorkommen. Ein Extrempunkt ist eine lokale Maximum- bzw. Minimumstelle.

Minimum- bzw. Maximumstellen lassen sich auch mithilfe von Ableitungen ermitteln:

Minimumstelle: f'(x) = 0 ∧ f''(x) > 0
Maximumstelle: f'(x) = 0 ∧ f''(x) < 0
Nullstelle: f(x) = 0

Sattelpunkt

In einem Sattelpunkt sinkt der Funktionswert weder, noch steigt er an. Sattelpunkte können bei Polynomfunktionen ab dem 3. Grad vorkommen. An einem Sattelpunkt gelten folgende Bedingungen:

Sattelstelle: f'(x) = 0 ∧ f''(x) = 0 ∧ f'''(x) ≠ 0

Wendestelle und Krümmung

An einer Wendestelle ändert eine Funktion ihr Krümmungsverhalten. Bei der Krümmung eines Funktionsgraphen kann positive bzw. Linkskrümmung, negative bzw. Rechtskrümmung oder auch keine Krümmung (an Wendestellen) auftreten. Auch Krümmung gibt man, wie Monotonie, in Intervallen an. An einer Wendestelle tritt maximale Steigung bzw. maximales Gefälle auf. Damit ein Punkt eine Wendestelle ist, muss folgendes gelten:

Wendepunkt: f''(x) = 0 ∧ f'''(x) ≠ 0, falls f(x) keine Sattelstelle ist

Änderungsmaße

Absolute Änderung

Die Änderung einer Funktion in [a; b] gibt an, um welchen Wert der Funktionswert in diesem Bereich gestiegen oder gesunken ist. Dabei sind alle Werte dazwischen irrelevant.

Absolute Änderung: f(b) - f(a)

Relative Änderung

Die Relative Änderung einer Funktion in [a; b] gibt an, um welchen Wert sich der Funktionswert in diesem Bereich relativ zum Ausgangswert f(a) ändert. Dabei sind wieder alle Werte dazwischen irrelevant.

Relative Änderung: $\frac{f(b) - f(a)}{f(a)}$

Wenn jetzt also f(a) = 10 und f(b) = 12 ist, erhalten wir laut der Formel 0,2 → der Funktionswert ist um den Ausgangswert f(a) ⋅ 0,2 bzw. 20% gestiegen.

Mittlere Änderungsrate bzw. Differenzenquotient:

Der Differenzenquotient gibt die durchschnittliche Änderung an jeder Stelle im Bereich [a; b] an, ohne den Werten dazwischen Beachtung zu schenken.

Mittlere Änderungsrate: $\frac{f(b) - f(a)}{b - a}$

Änderungsfaktor

Der Änderungsfaktor gibt an, mit welcher Zahl wir f(a) multiplizieren müssten, um auf f(b) zu kommen.

Änderungsfaktor: $\frac{f(b)}{f(a)}$

Geschwindigkeit und Änderungsgeschwindigkeit

Die mittlere Geschwindigkeit in einem Zeitintervall ist nichts anderes, als die Mittlere Änderungsrate der zurückgelegten Strecke im Intervall [a; b]. Die Geschwindigkeit zum Zeitpunkt t entspricht der Steigung der Funktion und somit der ersten Ableitung s'(t).

Diese Geschwindigkeit lässt sich nun auch ausweiten auf allgemein die Änderung des Funktionswertes - z.B. eine Volumensänderung. Hier geht es nur nicht um die zurückgelegte Strecke, sondern z.B. darum, wie schnell ein Behälter sich füllt oder leert. Auch hier ist die mittlere Änderungsgeschwindigkeit im Intervall [a; b] nichts anderes, als die mittlere Änderungsrate der Funktion im Intervall [a; b] und die momentane Änderungsgeschwindigkeit nichts anderes als die Steigung der Funktion und somit die erste Ableitung V'(t). Ist diese positiv, spricht man von der (mittleren) Zunahmegeschwindigkeit, ist sie negativ, so von der (mittleren) Abnahmegeschwindigkeit.

Differentialquotient

Diese eben erwähnte (momentane) Änderungsgeschwindigkeit einer Funktion bzw. die Steigung des Funktionsgraphen nennt man Differentialquotient, er wird mithilfe der ersten Ableitung f'(x) berechnet.

Leibniz-Ableitung

Die Leibniz'sche Schreibweise ist eine andere Schreibweise der Ableitung (hier wird nur die erste Ableitung benötigt) einer Funktion. Besonders praktisch ist sie bei Funktionen mit mehreren Variablen bzw. physikalischen Formeln, wenn angenommen wird, dass alle Variablen der Formel konstant bleiben, mit Ausnahme einer. Nach dieser Variable wird dann abgeleitet. Also: $\frac{dV}{dN}$ → Leite V nach N ab. Schauen wir uns das an einem Beispiel an:

p ⋅ V = N ⋅ k ⋅ T
Angabe: $\frac{dV}{dN}$
Also: Leite V nach N ab.
Dafür stellen wir erstmal V frei:
$V = \frac{N ⋅ k ⋅ T}{p}$
Wir leiten nach N ab, und da N¹ wegfällt, erhalten wir:
V'(N) = $\frac{dV}{dN} = \frac{k ⋅ T}{p}$