Mathe-SA am 12.06.2025

Funktionen und Graphen

Funktionsgraphen

Name	Funktionsgleichung	Graph
Lineare Funktion	f(x) = k ⋅ x + d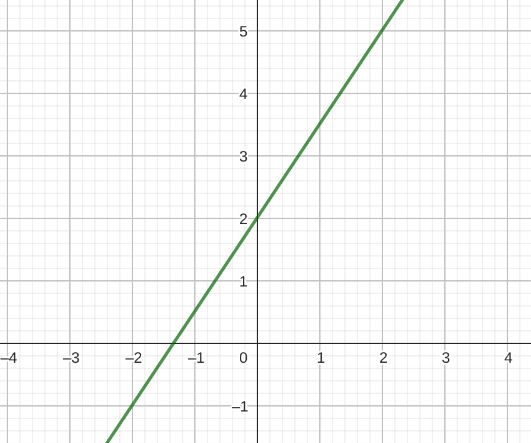
Quadratische Funktion	f(x) = a ⋅ x2 + b ⋅ x + c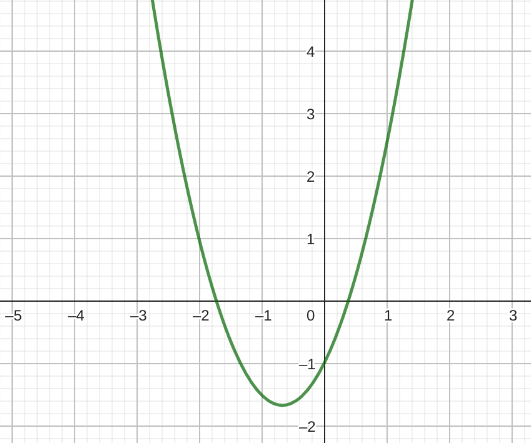
Exponentialfunktion	f(x) = ax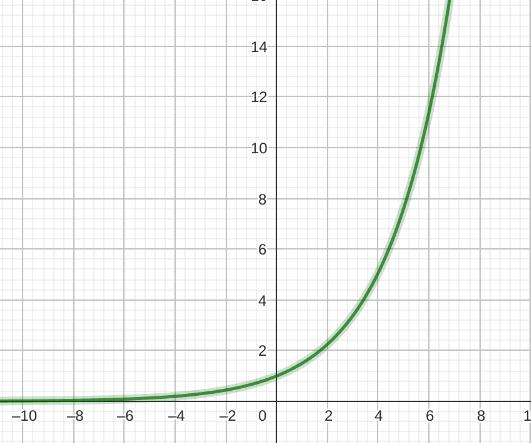
Logarithmusfunktion	f(x) = logn(x)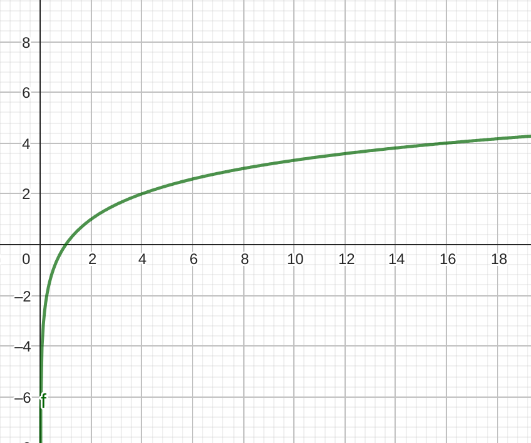
Potenzfunktion Falls n ungerade: "S"-Form Falls n gerade: "W" oder "M"-Form	f(x) = a ⋅ xn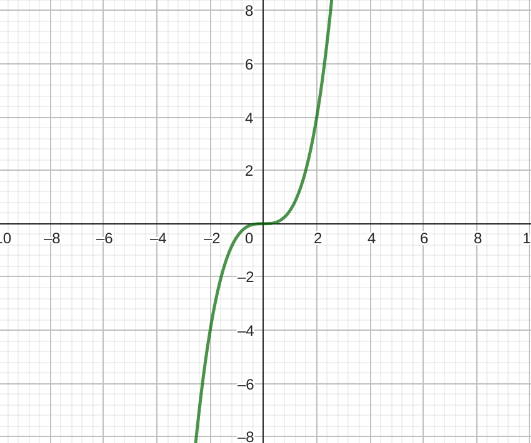
Polynomfunktion Wie bei Potenzfunktion: Falls n gerade: "W" oder "M"-Form Falls n ungerade: "S"-Form	f(x) = a0 ⋅ xn + a1 ⋅ xn-1+ ... + an ⋅ x0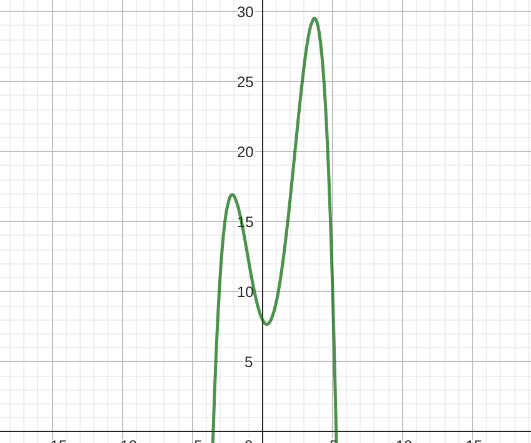

Winkelfunktionen

Sinus- und Cosinusfunktion

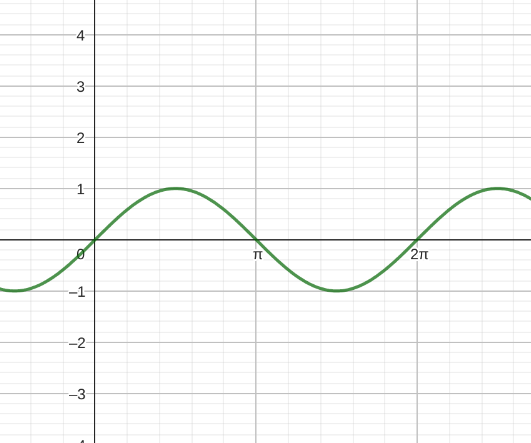
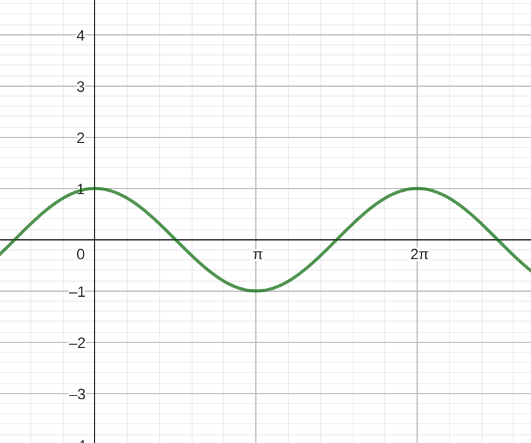
Winkelfunktionen sind Sinus-, Cosinus-, und Tangensfunktion. Diese sehen in der Grundfunktion (Amplitude = 1, keine Phasenverschiebung) folgendermaßen aus:

Sinusfunktion	Cosinusfunktion	Tangensfunktion

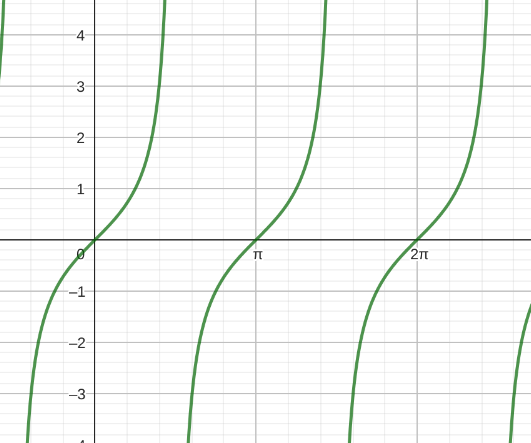Wie man sieht, haben die Sinus- und Cosinusfunktion eine Periode von 2π und die Tangensfunktion eine Periode von π. Die Cosinusfunktion können wir auch als eine Phasenverschobene Sinusfunktion schreiben:

sin(x) = cos(x - $\frac{\pi }{2}$) bzw. cos(x) = sin(x + $\frac{\pi }{2}$)

Wie wir sehen, wird die Sinusfunktion bei einer Phasenverschiebung von + $\frac{\pi }{2}$ um $\frac{\pi }{2}$ nach links verschoben, die Cosinusfunktion bei negativer Phasenverschiebung nach rechts. Die Sinusfunktion sieht allgemein so aus: f(x) = a ⋅ sin(b ⋅ x + c). a ist die Amplitude, b die Kreisfrequenz, und c die Phasenverschiebung. b kann auch als ω und c als φ geschrieben werden (hauptsächlich in der Physik). Die Amplitude streckt/staucht die Funktion entlang der y-Achse, die Kreisfrequenz entlang der x-Achse. Die Phasenverschiebung verschiebt die Funktion entlang der x-Achse nach links oder rechts.

Schwingungen

Bei harmonischen Schwingungen (also Schwingungen, die durch eine Sinusfunktion s(t) = a ⋅ sin(b ⋅ t + c), also auch Cosinusfunktion, dargestellt werden können) kommen ein paar Begriffe hinzu:

• Elongation: Wert der Funktion zum Zeitpunt t
• Amplitude (a): Größtmögliche Elongation (höchster Punkt der Funktion)
• Schwingungsdauer (T): Zeit, die für eine vollständige Schwingung benötigt wird; ohne Kreisfrequenz ist sie 2π. T = $\frac{1}{f}$; T = $\frac{\mathrm{2\; \cdot \; \pi }}{\omega }$
• Frequenz: Anzahl an Schwingungen pro Sekunde; Einheit: Hz (Hertz). f = $\frac{1}{T}$; f = $\frac{\omega }{2\; \cdot \; \pi }$

Gleichungssysteme

Für die Schularbeit ist lediglich das Identifizieren eines Gleichungssystems aus einer Textaufgabe und das Lösen dieses Gleichungssystems mithilfe von GeoGebra erforderlich, deshalb wird hier nicht auf das Händische Lösen eingegangen.

Zunächst ist GeoGebra CAS zu öffnen: &9776; oben rechts → Perspektiven → CAS.