Mathe-SA am 12.06.2025
Funktionen und Graphen
Funktionsgraphen
| Name | Funktionsgleichung | Graph |
|---|---|---|
| Lineare Funktion | f(x) = k ⋅ x + d | 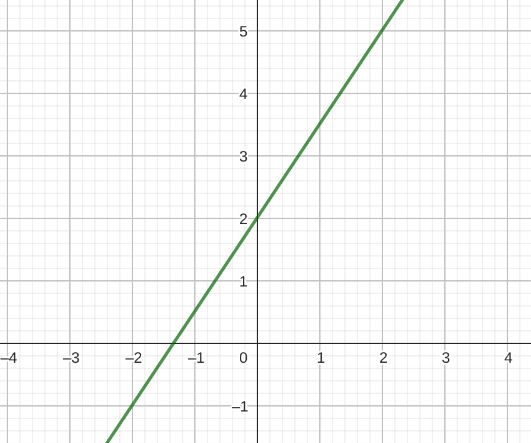 |
| Quadratische Funktion | f(x) = a ⋅ x2 + b ⋅ x + c | 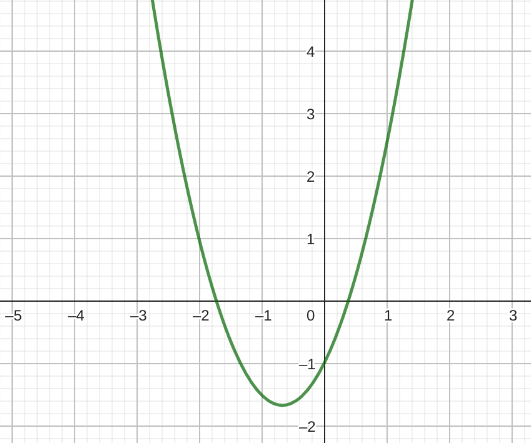 |
| Exponentialfunktion | f(x) = ax | 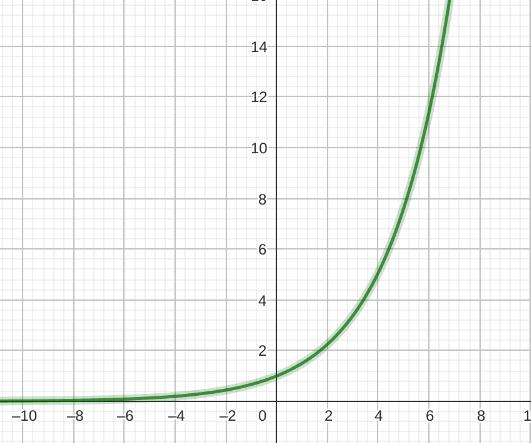 |
| Logarithmusfunktion | f(x) = logn(x) | 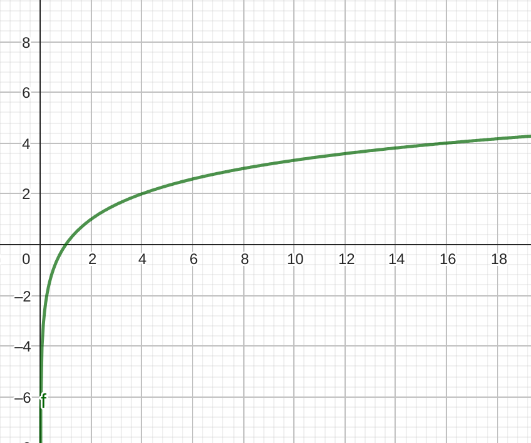 |
| Potenzfunktion Falls n ungerade: "S"-Form Falls n gerade: "W" oder "M"-Form |
f(x) = a ⋅ xn | 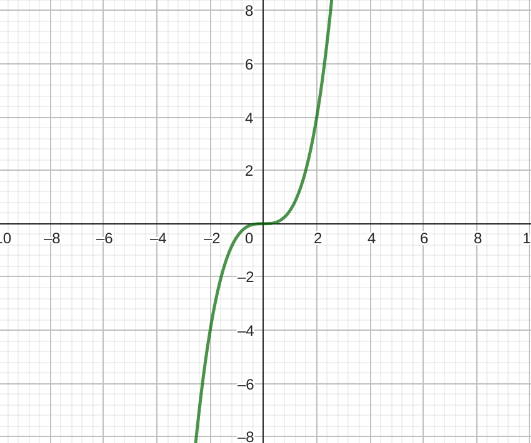 |
| Polynomfunktion Wie bei Potenzfunktion: Falls n gerade: "W" oder "M"-Form Falls n ungerade: "S"-Form |
f(x) = a0 ⋅ xn + a1 ⋅ xn-1+ ... + an ⋅ x0 | 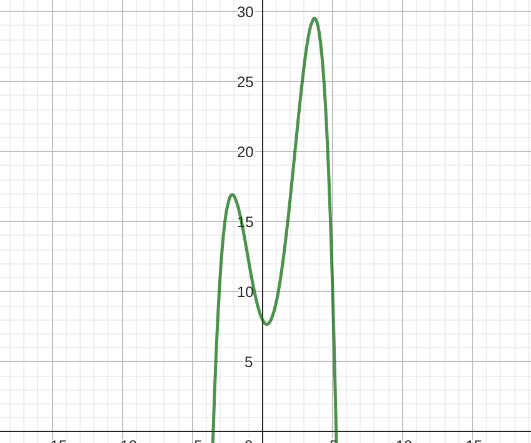 |
Winkelfunktionen
Sinus- und Cosinusfunktion
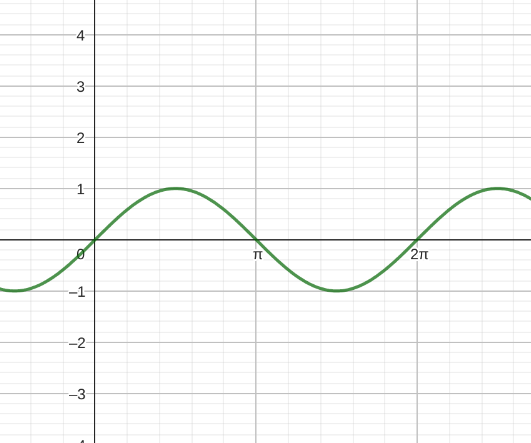
Winkelfunktionen sind Sinus-, Cosinus-, und Tangensfunktion. Diese sehen in der Grundfunktion (Amplitude = 1, keine Phasenverschiebung) folgendermaßen aus:
| Sinusfunktion | Cosinusfunktion | Tangensfunktion |
|---|---|---|
 |
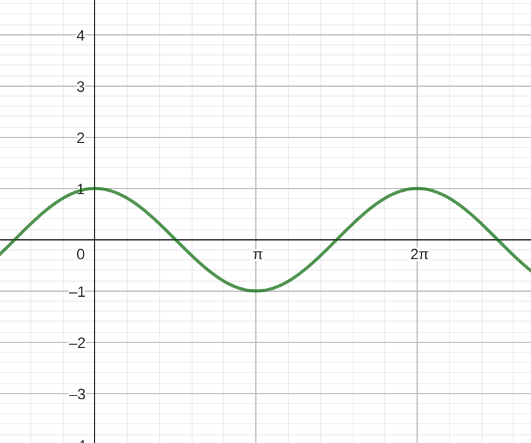 |
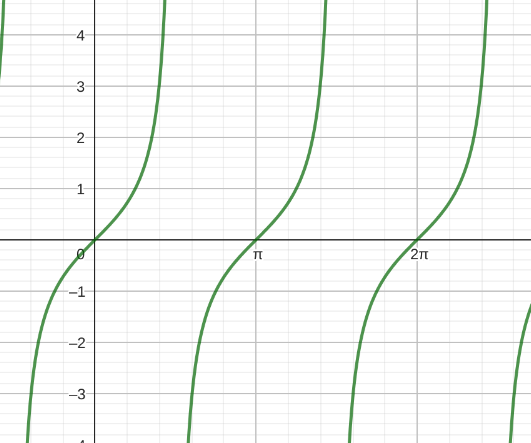 |
Wie man sieht, haben die Sinus- und Cosinusfunktion eine Periode von 2π und die Tangensfunktion eine Periode von π. Die Cosinusfunktion können wir auch als eine Phasenverschobene Sinusfunktion schreiben:
sin(x) = cos(x - )
undbzw. cos(x) = sin(x + )
Wie wir sehen, wird die Sinusfunktion bei einer Phasenverschiebung von + um nach links verschoben, die Cosinusfunktion bei negativer Phasenverschiebung nach rechts. Die Sinusfunktion sieht allgemein so aus: f(x) = a ⋅ sin(b ⋅ x + c). a ist die Amplitude, b die Kreisfrequenz, und c die Phasenverschiebung. b kann auch als ω und c als φ geschrieben werden (hauptsächlich in der Physik). Die Amplitude streckt/staucht die Funktion entlang der y-Achse, die Kreisfrequenz entlang der x-Achse. Die Phasenverschiebung verschiebt die Funktion entlang der x-Achse nach links oder rechts.
Schwingungen
Bei harmonischen Schwingungen (also Schwingungen, die durch eine Sinusfunktion s(t) = a ⋅ sin(b ⋅ t + c), also auch Cosinusfunktion, dargestellt werden können) kommen ein paar Begriffe hinzu:
- Elongation: Wert der Funktion zum Zeitpunt t
- Amplitude (a): Größtmögliche Elongation (höchster Punkt der Funktion)
- Schwingungsdauer (T): Zeitdauer, die für eine vollständige Schwingung benötigt wird; ohne Kreisfrequenz ist sie 2π. T = ; T =