Differentialrechnung

Eigenschaften von Funktionen

Monotonie

Bei normaler Monotonie darf der Funktionswert auch weder steigen noch sinken (gleich bleiben), bei strenger Monotonie muss er durchgehend fallen bzw. sinken:

	steigend	fallend
monoton	Funktionswert wird nicht kleiner	Funktionswert wird nicht größer
streng monoton	Funktionswert wird größer	Funktionswert wird kleiner

Für Montonie wird üblicherweise ein abgeschlossenes Intervall [a; b] angegeben, z.B.: f(x) ist in [a; b] streng monoton fallend.

Extremstellen

Ein Punkt auf einer Funktion in einem Intervall (oder auch allgemein) ist eine Maximumstelle, wenn es im gesamten Intervall keine größeren Funktionwerte gibt. Ein Punkt auf einer Funktion ist eine Minimumstelle, falls es im gesamten Intervall keine kleineren Funktionswerte gibt. Eine Extremstelle ist entweder eine Minimum- oder Maximumstelle der Funktion.

Ein Punkt ist eine lokale Maximumstelle oder Hochpunkt, falls es eine Umgebung des Punktes gibt, in der nur kleinere Funktionswerte vorkommen. Damit ein Punkt eine lokale Minimumstelle oder Tiefpunkt ist, muss es eine Umgebung des Punktes geben, in der nur größere Funktionswerte vorkommen. Ein Extrempunkt ist eine lokale Maximum- bzw. Minimumstelle.

Minimum- bzw. Maximumstellen lassen sich auch mithilfe von Ableitungen ermitteln:

Minimumstelle: f'(x) = 0 ∧ f''(x) > 0
Maximumstelle: f'(x) = 0 ∧ f''(x) < 0
Nullstelle: f(x) = 0

Sattelpunkt

In einem Sattelpunkt sinkt der Funktionswert weder, noch steigt er an. Sattelpunkte können bei Polynomfunktionen ab dem 3. Grad vorkommen. An einem Sattelpunkt gelten folgende Bedingungen:

Sattelstelle: f'(x) = 0 ∧ f''(x) = 0 ∧ f'''(x) ≠ 0

Wendestelle und Krümmung

An einer Wendestelle ändert eine Funktion ihr Krümmungsverhalten. Bei der Krümmung eines Funktionsgraphen kann positive bzw. Linkskrümmung, negative bzw. Rechtskrümmung oder auch keine Krümmung (an Wendestellen) auftreten. Auch Krümmung gibt man, wie Monotonie, in Intervallen an. An einer Wendestelle tritt maximale Steigung bzw. maximales Gefälle auf. Damit ein Punkt eine Wendestelle ist, muss folgendes gelten:

Wendepunkt: f''(x) = 0 ∧ f'''(x) ≠ 0, falls f(x) keine Sattelstelle ist

Um das Krümmungsverhalten einer Funktion zu analysieren, müssen zunächst alle Wendestellen ermittelt werden. Dann kann jeweils zwischen zwei Wendestellen bzw. an den Seiten der Wendestellen am Rand die Krümmung (zweite Ableitung f''(x)) und damit das Krümmungsverhalten (positiv/negativ) im betreffenden Bereich ermittelt werden. Gibt es keine Wendepunkte, kann einfach an einer beliebigen Stelle die Krümmung ermittelt werden, diese gilt für die gesamte Funktion (da es ja keine Wendepunkte gibt, an denen das Krümmungsverhalten sich ändern würde).

Änderungsmaße

Absolute Änderung

Die Änderung einer Funktion in [a; b] gibt an, um welchen Wert der Funktionswert in diesem Bereich gestiegen oder gesunken ist. Dabei sind alle Werte dazwischen irrelevant.

Absolute Änderung: f(b) - f(a)

Relative Änderung

Die Relative Änderung einer Funktion in [a; b] gibt an, um welchen Wert sich der Funktionswert in diesem Bereich relativ zum Ausgangswert f(a) ändert. Dabei sind wieder alle Werte dazwischen irrelevant.

Relative Änderung: $\frac{\mathrm{f(b)\; -\; f(a)}}{\mathrm{f(a)}}$

Wenn jetzt also f(a) = 10 und f(b) = 12 ist, erhalten wir laut der Formel 0,2 → der Funktionswert ist um den Ausgangswert f(a) ⋅ 0,2 bzw. 20% gestiegen.

Mittlere Änderungsrate bzw. Differenzenquotient:

Der Differenzenquotient gibt die durchschnittliche Änderung an jeder Stelle im Bereich [a; b] an, ohne den Werten dazwischen Beachtung zu schenken.

Mittlere Änderungsrate: $\frac{\mathrm{f(b)\; -\; f(a)}}{\mathrm{b\; -\; a}}$

Änderungsfaktor

Der Änderungsfaktor gibt an, mit welcher Zahl wir f(a) multiplizieren müssten, um auf f(b) zu kommen.

Änderungsfaktor: $\frac{\mathrm{f(b)}}{\mathrm{f(a)}}$

Geschwindigkeit und Änderungsgeschwindigkeit

Die mittlere Geschwindigkeit in einem Zeitintervall ist nichts anderes, als die Mittlere Änderungsrate der zurückgelegten Strecke im Intervall [a; b]. Die Geschwindigkeit zum Zeitpunkt t entspricht der Steigung der Funktion und somit der ersten Ableitung s'(t).

Diese Geschwindigkeit lässt sich nun auch ausweiten auf allgemein die Änderung des Funktionswertes - z.B. eine Volumensänderung. Hier geht es nur nicht um die zurückgelegte Strecke, sondern z.B. darum, wie schnell ein Behälter sich füllt oder leert. Auch hier ist die mittlere Änderungsgeschwindigkeit im Intervall [a; b] nichts anderes, als die mittlere Änderungsrate der Funktion im Intervall [a; b] und die momentane Änderungsgeschwindigkeit nichts anderes als die Steigung der Funktion und somit die erste Ableitung V'(t). Ist diese positiv, spricht man von der (mittleren) Zunahmegeschwindigkeit, ist sie negativ, so von der (mittleren) Abnahmegeschwindigkeit.

Differentialquotient

Diese eben erwähnte (momentane) Änderungsgeschwindigkeit einer Funktion bzw. die Steigung des Funktionsgraphen nennt man Differentialquotient, er wird mithilfe der ersten Ableitung f'(x) berechnet.

Leibniz-Ableitung

Die Leibniz'sche Schreibweise ist eine andere Schreibweise der Ableitung (hier wird nur die erste Ableitung benötigt) einer Funktion. Besonders praktisch ist sie bei Funktionen mit mehreren Variablen bzw. physikalischen Formeln, wenn angenommen wird, dass alle Variablen der Formel konstant bleiben, mit Ausnahme einer. Nach dieser Variable wird dann abgeleitet. Also: $\frac{\mathrm{dV}}{\mathrm{dN}}$ → Leite V nach N ab. Schauen wir uns das an einem Beispiel an:

p ⋅ V = N ⋅ k ⋅ T
Angabe: $\frac{\mathrm{dV}}{\mathrm{dN}}$
Also: Leite V nach N ab.
Dafür stellen wir erstmal V frei:
$V = \frac{\mathrm{N\; \cdot \; k\; \cdot \; T}}{\mathrm{p}}$
Wir leiten nach N ab, und da N¹ wegfällt, erhalten wir:
V'(N) = $\frac{\mathrm{dV}}{\mathrm{dN}} = \frac{\mathrm{k\; \cdot \; T}}{\mathrm{p}}$

Ableitungsregeln

f'(x) nennt man Ableitung oder Ableitungsfunktion von f(x), das Berechnen einer Ableitung Ableiten bzw. Differenzieren. Dabei schauen wir uns folgendes an:

• die Variable selbst (z.B. x)
• Konstanten, mit denen sie multipliziert wird
• Konstanten, die addiert werden

Folgende Regeln sind zu beachten:

• Konstanten, die addiert und nicht mit der Variable multipliziert werden, fallen weg. Das gilt auch, wenn mehrere solche Konstanten untereinander multipliziert werden - sie könnten als eine Konstante zusammengefasst werden.
• Die Variable fällt weg, falls sie den Exponenten 1 hat (x¹); Zahlen, mit denen sie multipliziert wird bleiben stehen (z.B. 3 ⋅ x¹ → 3).
• Ansonsten wird der Exponent der Variable um 1 reduziert und sie mit diesem multipliziert, auch ggf. andere Zahlen, mit denen die Variable ohnehin schon multipliziert wird (z.B. x³ → 3 ⋅ x²; 5 ⋅ x² → 10 ⋅ x¹).

Also gilt:

f(x) = xⁿ → f'(x) = n ⋅ x^n-1
f(x) = a ⋅ x^b → f'(x) = a ⋅ b ⋅ x^b-1
f(x) = a ⋅ x → f'(x) = a
f(x) = a → f'(x) = 0

Ableitungen in der Physik

Die Ableitungen haben auch physikalische Bedeutungen, z.B. bei einer Funktion, die die zurückgelegte Strecke zum Zeitpunkt t angibt s(t):

• Erste Ableitung s'(t): Geschwindigkeit zum Zeitpunkt t
• Zweite Ableitung s''(t): Beschleunigung zum Zeitpunkt t

Die erste Ableitung der Geschwindigkeitsfunktion v(t) ist die Beschleunigung. Auch geometrisch haben sie eine Bedeutung (bei einem Funktionsgraphen): f'(x) ist die Steigung und f''(x) die Krümmung an der Stelle x.

Polynomfunktionen aufstellen

Mithilfe der obigen Bedingungen können wir mithilfe von manchen Informationen über den Graphen (z.B. geht durch Punkt (x | y), Sattelstelle (x | y),...) ein Gleichungssystem und daraus die Polynomfunktion dazu aufstellen, besonders, wenn, wie bei den Beispielen hier, der Grad der Polynomfunktion angegeben ist. Dieses Gleichungssystem können wir auch mithilfe von GeoGebra lösen lassen, genauso wie wir GeoGebra auch zum Ermitteln von Sattelstellen, etc. bei bereits gegebenen Funktionen verwenden können - mit der Löse-Funktion. Schauen wir uns das Schritt für Schritt an:

Wir suchen zunächst einmal Bedingungen. Wir benötigen immer eine Bedingung mehr als den Grad der gesuchten Polynomfunktion. Z.B.:
Die Polynomfunktion vom Grad 3 hat den Tiefpunkt (3 | 1) und die Steigung der Tangente im Punkt P = (0 | 1) beträgt 3.
Daher können wir folgende Bedingungen aufschreiben:

• f(3) = 1, weil der Graph durch den Punkt (3 | 1) geht
• f(0) = 1, weil der Graph durch den Punkt (0 | 1) geht
• f'(3) = 0, weil die Steigung im Tiefpunkt (3 | 0) 0 ist
• f'(0) = 3, weil die Steigung im Punkt (0 | 1) 3 ist

Leiten wir die Funktion für den nächsten Schritt ersteinmal ab: f'(x) = 3 ⋅ a ⋅ x² + 2 ⋅ b ⋅ x + c
Jetzt können wir uns mithilfe dieser Bedingungen ein Gleichungssystem aufstellen:

• f(3) = a ⋅ 3³ + b ⋅ 3² + c ⋅ 3 + d = 1
• f(0) = a ⋅ 0³ + b ⋅ 0² + c ⋅ 0 = 1
• f'(3) = 3 ⋅ a ⋅ 3² + 2 ⋅ b ⋅ 3 + c = 0
• f'(0) = 3 ⋅ a ⋅ 0 + 2 ⋅ b ⋅ 0 + c = 3

Dieses Gleichungssystem können wir nun entweder händisch lösen oder in GeoGebra eintippen und lösen lassen.

Um eine Polynomfunktion mithilfe von GeoGebra lösen zu können, müssen wir nur die Bedingungen ermitteln, wie z.B. f'(3) = 0, f(5) = 0 oder f''(7) = 3, GeoGebra leitet ab und löst automatisch für uns:

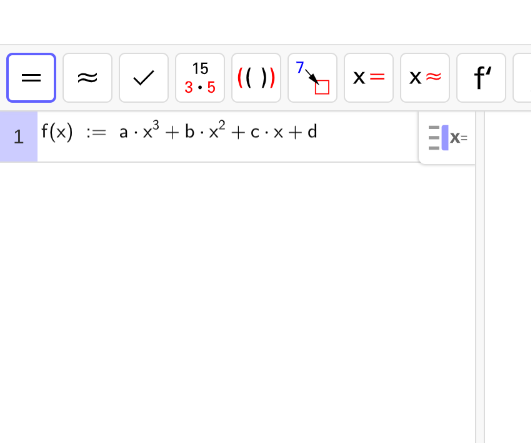
Zunächst einmal tippen wir die Form der Polynomfunktion ein, z.B. hier im 3. Grad, und bestätigen mit "Enter":



Dann tippen wir unsere Bedingungen ein:



Schlussendlich wählen wir alle Bedingungen (nicht unsere Polynomfunktion - hier an Stelle 1) aus und klicken im Menü oben links auf "x =", GeoGebra berechnet die Lösung nun automatisch für uns: